I calculate there are 25 outcomes from two spins, of which only five yield a score of 5 or more, equating to a 20% chance.
So, on 200 games, their total income is £50 (200 x £0.25).
They would expect to pay out on 20%, or 40, of those games.
Therefore, they would expect their total outlay to be £40 (40 x £1).
Their expected profit is £10 from 200 games (ie £50 less £40).
However, I’m also sure they expect their Grandfather to bail them out if the spinner doesn’t behave.
A very clear explanation. I always like a good explanation, probably more than seeing the answer.
Your observation prompts a harder spin-off question:
What is the probability of Don being out of pocket (assuming he agrees to this!) and what are his expected losses?
Well done Steve
As Ravvie said, a very clear explanation. And the correct answer, of course !
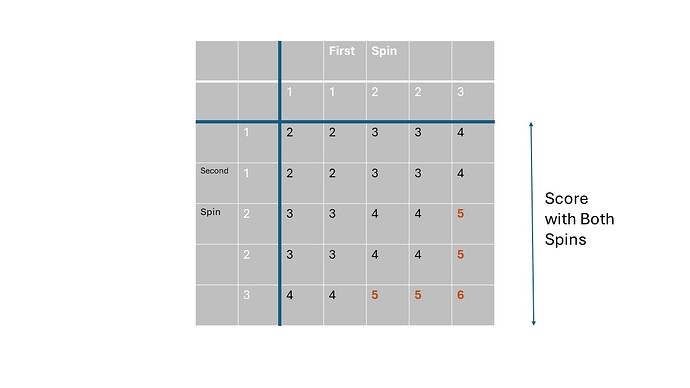
For the benefit of others who might be browsing, I have drawn up a grid to show the possible scores with two spins ie the 25 outcomes that Steve referred to. Five of these are coloured red to highlight those with a score of 5 or more.
Hmm, I’m struggling to work out a correct approach here. I can see that the maximum loss is £150, if every game results in a £1 payout (income £50 less payout £200).
The chances of this are presumably 0.2 to the power 200.
I seem to remember a binomial expansion, including Pascal’s Triangle, that would compute the odds every other individual occurrence (eg 199 lose - 1 win, 198 lose - 2 win etc etc).
However, I’ve no idea how you condense these calculations into something manageable.
Yes it is a binomial expansion and Pascal’s Triangle is a good tool to use, so you are on the right lines. It was the approach I used.
I did resort to using a spreadsheet to do the calculations though, given we need the 200th row. There is a shortcut that avoids having to create the whole triangle.
Whilst I can see how to approach it, the magnitude o the calculations are beyond me.
I’d be very happy to see your solution.
Similar situation over here Steve.
Raking through my memory, i have a vague recollection of a generalised formula. But things like (1/5)^200 or 200! are too small or too large to manage.
And i would have to do the calcs about 200 times and sum all 200 probabilities. My version of Excel wouldn’t cope, never mind my old Casio calculator or my squared note paper !!!
PS. I’ll have to check the above, I produced it in haste !
I also recollect using something similar to "estimate how many times you need to roll a fair dice to have a (say) better than 95% probability of getting a six.
Surprising what you can forget !!
I suggested to Mrs R that I would use a modified Pascal’s Triangle. She frowned as she always hates it when I go off-piste. Off the top of her head she gave me the formula I should use instead (same as Don’s formula). I pointed out the challenge of large factorials and it would need a lot of them, which she did concede. It does seem that we are all thinking on similar lines.
Even though sacrilege in some parts of the R household, modifying Pascal’s Triangle was actually quite simple in Excel, though harder to explain. I’ll leave it for now unless anyone is interested. It gave an answer that the probability of Don having to bail out his grandsons is 3.45%, with an expected loss of just 10 pence.
Let’s check it using an equivalent formula to the one Don provided.
I started with the case where Don is out of pocket by £1 (51 wins). Excel can’t calculate 200!/51!/149!, but it is ok with COMBIN(200,51). The probability is:
COMBIN(200,51) x 4^149 / 5^200 = 1.3349E+48 x 5.0926E+89 / 6.2230E+139 = 1.092%
I then increased the number of wins by 1 each time until the probability became negligible. No need for any further combinatorics or factorials as there is a simple relationship from Don’s formula. My calculations are:
| Wins | Loss £ | Multiply | Divide | Probability | Prob x Loss (£) |
|---|---|---|---|---|---|
| 51 | 1 | 1.092% | 0.0109 | ||
| 52 | 2 | 149 | 208 | 0.783% | 0.0157 |
| 53 | 3 | 148 | 212 | 0.546% | 0.0164 |
| 54 | 4 | 147 | 216 | 0.372% | 0.0149 |
| 55 | 5 | 146 | 220 | 0.247% | 0.0123 |
| 56 | 6 | 145 | 224 | 0.160% | 0.0096 |
| 57 | 7 | 144 | 228 | 0.101% | 0.0071 |
| 58 | 8 | 143 | 232 | 0.062% | 0.0050 |
| 59 | 9 | 142 | 236 | 0.037% | 0.0034 |
| 60 | 10 | 141 | 240 | 0.022% | 0.0022 |
| 61 | 11 | 140 | 244 | 0.013% | 0.0014 |
| 62 | 12 | 139 | 248 | 0.007% | 0.0008 |
| 63 | 13 | 138 | 252 | 0.004% | 0.0005 |
| Total: | 3.445% | 0.1001 |
This agrees with my other method which in graph form gave:
The grandsons are expected to win £10.10 and Don expected to lose £0.10, agreeing in total with the answer to the original teaser.
![]()
![]()
![]() Chapeau!
Chapeau!
Hi Ravvie,
As Steve says, well done !
You can read that as “Well Done Factorial” ![]()
Sequences
After the trauma of possibly loosing 10p in the previous teaser (nice one Ravvie) ![]()
I thought something more straight forward might be appropriate !
The numbers above, form a sequence running from left to right.
Which number should replace the question mark ?
PS. I’ve only ‘wiggled’ the line to make it look more interesting !
I think 42, as the missing numbers appear to be prime numbers, so no 41.
Mrs R got 42 also, a bit ahead of me.
She dropped the hint that I would get it if I was in the prime of my life.
Isn’t the answer to the universe 42.
Well spotted Pete !!
Well done Steve. And nicely explained.
Looks like you might have just achieved that status !!
Following on from the “21 … to … 42” sequence, I also created two additional similar sequences.
I was really surprised to note that the sequence of Primes v non-Primes was precisely the same in all three sequences.
I’ll post them later today or tomorrow, unless someone else gets there before hand ![]()
Here are my three sequences.
They are not actually startling, but I hadn’t really noticed before, just how regularly some of the early primes appear in the overall number sequence.
Of course, if I hadn’t omitted the 43-50 and 73-80 parts of the overall number sequence, there are a few anomalies !