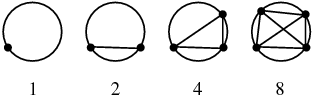Agreed, I don’t feel a division between us.
For those who might still be wondering how that last sequence works 
1500 divided by 9, then 8, then 7, then 6 …
Well done Ravvie - you certainly need to be ultra quick when Eoink is about !!!
In the past, some of these teasers have required days, or even weeks, of team effort to sort out. Take the “Ladder” teaser that I posted way back in this thread, and which remains unsolved. And if you go back even further, to the first Brain Teaser thread way back c.2000, you will find even better examples of real teamwork getting to the heart of some difficult teasers.
A Piece of Cake (or maybe not)
This is a puzzle from my student days. Maybe one for team work as there are several aspects to it.
Points are marked on the edge of a circular cake and straight lines are cut between each and every edge point, creating an increasing number of cake pieces. The diagram shows how the cake might look after the first few points:
( A ) What must one do (or not do) to maximise the number of cake pieces for a given number of edge points?
( B ) What is the maximum number of cake pieces for each of 5 and 6 edge points?
( C ) What about 7 or more?
( D ) Can we reach 10?
( E ) A general formula or method that works for any number?
OK, I’ll give it a start.
I can see some sort of pattern emerging with points running from 1 thru 7. The following are the number of resulting pieces of cake. The first number being the pieces of cake that have one curved edge. All the remaining pieces have straight edges.
1
2
3 1
4 4
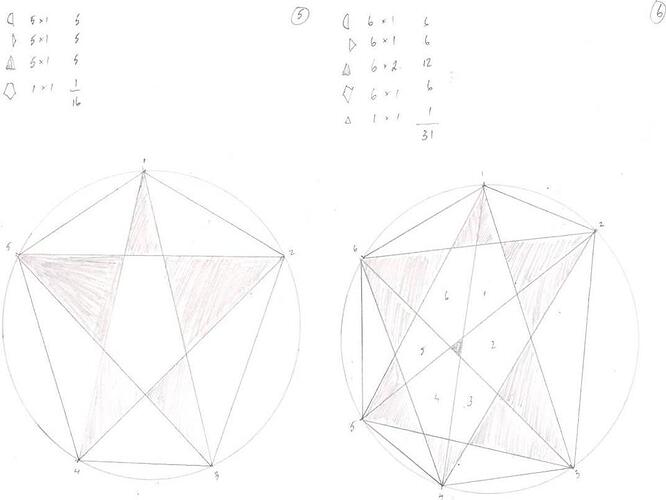
5 10 1
6 18 6 1
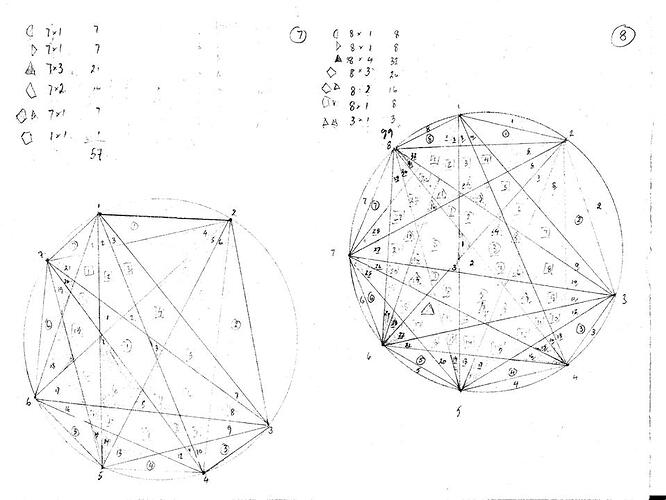
7 28 14 7 1
Giving totals of 1, 2, 4, 8, 16, 31, 57
I have avoided allowing more than two lines to intersect
@Don has made a good start. Everything is correct so far.
When I saw this puzzle originally, it took me some time to accept that the next number after 1, 2, 4, 8, 16 was 31 rather than 32.
I had hoped for a bit of help … 
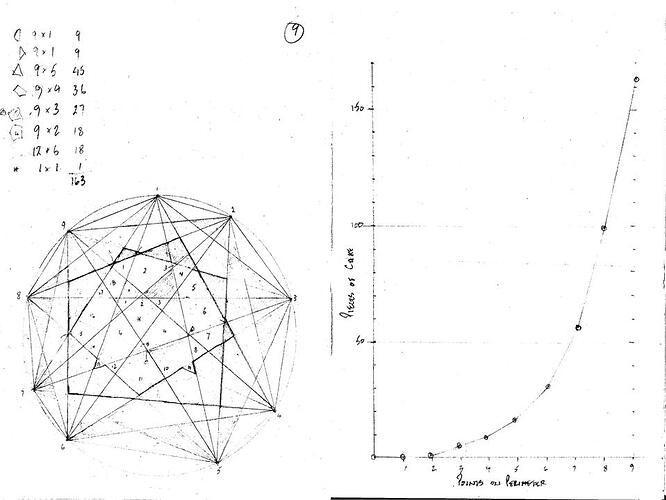
My next two numbers, for 8 and then 9 dots on the perimeter are 99 and 163 respectively.
So far, my sequence is 1, 2, 4, 8, 16, 31, 57, 99, 163
I think I can see a formula developing, but it isn’t pretty !!!
But it does generate the above numbers, which I initially got by simply drawing out the circles with 5, 6, 7, 8 then 9 dots around the perimeter, then drawing the cut-lines and carefully counting the pieces.
I’ve just realised that for 10 dots on the perimeter, my embrionic formula is such that I could probably do the arithmetic in my head, but I will use my calculator nevertheless.
Trying to do a drawing to prove that my formula works for 10 dots is going to need an A1 sheet of paper and the spare wheel from the SUV 
Well, that was easier than I thought and generated 256, which seems a remarkable co-incidence given that the sequence started off with 1, 2, 4, 8, 16 …
But the formula works for 1 to 9 and it looks reassuringly complicated !!
I gave it a shot for 100 points …
Answer = 3,926,176 pieces of cake.
No way could I verify that with a drawing 
Well done, @Don!
I agree with your calculations for 100 points (as well as all the other results). It’s just as well that you can do maths as otherwise you would need a forest of paper and a larger SUV!
Did you develop the approach you outlined in your first response? I tried extending it to 8 points and could see some pattern emerging but I couldn’t get a complete picture that worked.
I’ll post my raw drawings below for 5, 6, 7, 8 and 9 points on the circle.
As I built up a record of the pieces of cake, I could see some sort of pattern developing when I had got to 7 points. I posted that a few days ago. It seemed to me that it might form part of a Pascal Triangle.
However, with 8 points, the “1” at the end (centre of the cake) became “3”. Worse still, the areas towards the centre of the 9 point cake seemed to lend themselves to 12 + 6 rather than 9 + 9.
And of course, the 4 point cake always had that annoying anomaly of just being 4 + 4
The pictures aren’t very good.
However, the graph gave me hope that I could find some sort of polynomial to describe it.
Some of those pieces of cake aren’t worth fighting over…
Mike,
If Don makes a cake as big as his SUV wheel, then I would like a piece of it!
Don,
How did you deal with the anomalies and how did Pascal’s Triangle tie in?
Well, I drew out Pascal’s Triangle to the line
1 10 45 120 210 252 210 120 45 10 1
After a bit of “day-dreaming” I noticed that if you started adding up the numbers on the horizontal lines, lines 1 thru 5 generated the solutions for circles with 1 thru 5 dots on the perimeter.
However, line 6, gave 32 … unless you dropped the “1” at the end, thus giving 31
And then I noticed that line 7 gave 64 … unless you dropped the “6” and the “1” at the end, thus giving 57
So I tried adding up the numbers along each line and found that I always got to the exact number of pieces of cake (from my pictures) before I got to the end of the line.
Then a bit more “day-dreaming” and I noticed that I could draw a straight “diagonal” line through Pascal’s Triangle so as to discard the unwanted numbers.
I’ll attach the diagram I used, below.
Well, that shows great vision.
It also shows why it is dangerous to assume (as I did initially) that a pattern of 1, 2, 4, 8, 16 would “clearly” be followed by 32.
Any thoughts on why Pascal’s Triangle works in this way?